Abstract
We investigate the nondegeneracy of higher order Levi forms on weakly nondegenerate homogeneous CR manifolds. Improving previous results, we prove that general orbits of real forms in complex flag manifolds have order less or equal than 3 and the compact ones less or equal 2. Finally we construct by Lie extensions weakly nondegenerate CR vector bundles with arbitrary orders of nondegeneracy.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Levi form is a basic invariant of CR geometry (see e.g. [9]). It is a hermitian symmetric form on the space of tangent holomorphic vector fields, which, when the CR codimension is larger than one, is vector valued. Its nondegeneracy was shown in [25] to be a sufficient condition to apply Cartan’s method to investigate equivalence and automorphisms of CR structures and is an obvious obstruction for locally representing the manifold as a product of a CR manifold of smaller dimension and of a nontrivial complex manifold. Sufficient more general conditions preventing a CR manifold \(\textsf {M}\) from being foliated by complex leaves of positive dimension or from having an infinite dimensional group of local CR automorphisms can be expressed by the nondegeneracy of higher order Levi forms (see e.g. [12, 13]). In the case of homogeneous CR manifolds these properties can be rephrased in terms of their associated CR algebras and lead to the notions of weak nondegeneracy and ideal nondegeneracy in [21]. The last one was renamed contact nondegeneracy and proved sufficient for the finite dimensionality of the group of CR automorphisms in [18].
Iterations of the Levi forms can be described by building descending chains of algebras of vector fields, whose lengths can be taken as a measure of nondegeneracy (see Sect. 1.1). One of these numbers, that we call here Levi order, and relates to weak nondegeneracy, is the main topic of this paper. The real submanifolds \(\textsf {M}\) of a complex flag manifold \(\textsf {F}\) of a semisimple complex group \(\mathbf {S}\) that are orbits of its real form \(\mathbf {S}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) form an interesting class of homogeneous CR manifolds, that has been studied e.g. in [1, 3]. In [10] G. Fels showed that when the isotropy \(\mathbf {Q}\) of \(\textsf {F}\) is a maximal parabolic subgroup, and \(\textsf {M}\) is weakly nondegenerate, then its Levi order is at most 3 and found an example where it is in fact equal to 3. In Sect. 2 we prove that this bound is valid for general weakly nondegenerate real orbits, dropping the maximality assumption on \(\mathbf {Q}\) and give further examples of weakly nondegenerate real orbits having Levi order 3. Moreover we show that the minimal orbit (the single one which is compact, cf. [27]) cannot have a finite Levi order larger than 2 and that the same result is valid for a larger class or orbits, that we name of the minimal type. Orbits which are not of the minimal type may have any finite order 1, 2, 3. Our methods are illustrated by several examples. We point out that, together with the new results obtained here, those in [1], where descriptions in terms of cross-marked Satake diagrams are emphasised, would allow to list all minimal orbits of Levi orders 1 and 2.
In [10] Fels posed the question of the existence of weakly nondegenerate homogeneous CR manifolds with Levi order larger than 3. In Sect. 3 we exhibit, by constructing some CR vector bundles over \(\mathbb {CP}^{1}\), weakly nondegenerate homogeneous CR manifolds having Levi order  for every positive integer
for every positive integer  .
.
2 Nondegeneracy conditions
2.1 Abstract CR manifolds
In this subsection we discuss some notions of nondegeneracy for general smooth abstract CR manifolds of type (n, k). We will eventually be interested in the locally homogeneous case and therefore, in the rest of this section, in their reformulation in the framework of Lie algebras theory.
We recall that an abstract CR manifold of type (n, k) is defined by the datum, on a smooth manifold \(\textsf {M}\) of real dimension \(2n{+}k,\) of a rank n smooth complex linear subbundle \(\textsf {T}^{0,1}\textsf {M}\) of its complexified tangent bundle \(\textsf {T}^{{{\,\mathrm{\mathbb {C}}\,}}}\textsf {M},\) satisfying
and the formal integrability condition
Set
The rank 2n real subbundle \(\textsf {H}\textsf {M}\) of \(\textsf {T}\textsf {M}\) is the real contact distribution underlying the CR structure of \(\textsf {M}.\)
A smooth \({{\,\mathrm{{\mathbb {R}}}\,}}\)-linear bundle map \(\mathrm {J}_{\textsf {M}}:\textsf {H}\textsf {M}\rightarrow \textsf {H}\textsf {M}\) is defined by the equation

The map \(\mathrm {J}_{\textsf {M}}\) squares to \(-\mathrm {I}_{\textsf {H}}\) and is the partial complex structure of \(\textsf {M}.\)
An equivalent definition of the CR structure can be given by assigning first an even dimensional distribution \(\textsf {H}\textsf {M}\) and then a smooth partial complex structure \(\mathrm {J}_{\textsf {M}}\) on \(\textsf {H}\textsf {M}\) in such a way that the complex distribution (1.4) satisfies (1.2).
Let us denote by  (resp.
(resp. 
 ,
, 
 ) the sheaf of germs of smooth sections of \(\textsf {H}\textsf {M}\) (resp. \(\textsf {T}\textsf {M},\) \(\textsf {H}^{{{\,\mathrm{\mathbb {C}}\,}}}\textsf {M},\) \(\textsf {T}^{0,1}\textsf {M},\) \(\textsf {T}^{1,0}\textsf {M}\)).
) the sheaf of germs of smooth sections of \(\textsf {H}\textsf {M}\) (resp. \(\textsf {T}\textsf {M},\) \(\textsf {H}^{{{\,\mathrm{\mathbb {C}}\,}}}\textsf {M},\) \(\textsf {T}^{0,1}\textsf {M},\) \(\textsf {T}^{1,0}\textsf {M}\)).
Definition 1.1
A CR manifold \(\textsf {M}\) is called fundamental at its point x if  generates the Lie algebra
generates the Lie algebra 
We define recursively a nested sequence of sheaves of germs of smooth complex valued vector fields on \(\textsf {M}\)

by setting

By conjugation we obtain another nested sequence of sheaves

where

These sequences, considered by Freeman in [12, Thm.3.1], correspond to the chain (1.11) that we construct in the locally homogeneous case.
In the same paper (cf. [12, Remarks 4.5]) also another sequence, introduced before in [15, 16], was considered, which will correspond to (1.15), namely

with

Definition 1.2
The CR manifold \(\textsf {M}\) has, at its point x,
-
Levi order
 if
if  ;
; -
contact order
 if
if 
We say that \(\textsf {M}\) is, at its point x
-
Levi (resp. contact) nondegenerate if it has Levi (resp. contact) order 1;
-
weakly (resp. contact) nondegenerate if it has finite Levi (resp. contact) order
 ;
; -
holomorphically (resp. contact) degenerate if it is not weakly (resp. contact) nondegenerate.
The Levi order at x is the smallest  for which, given any nonzero germ
for which, given any nonzero germ  we can find a
we can find a  and
and  such that
such that

The contact order can be defined in the same way, but with  taken in
taken in  We have therefore
We have therefore
Proposition 1.1
Let us keep the notation introduced above. Fix a point x in \(\textsf {M}.\) Then:
-
\(\textsf {M}\) has Levi order 1 at x if and only if it has contact order 1 at x.
-
If \(\textsf {M}\) has finite Levi order
 at x, then it has also finite contact order
at x, then it has also finite contact order  with
with 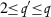 at x. \(\square \)
at x. \(\square \)
2.2 Homogeneous CR manifolds and CR algebras
Let \({{\,\mathrm{\mathbf {G}}\,}}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) be a Lie group of CR diffeomorphisms acting transitively on a CR manifold \(\textsf {M}.\) Fix a point x of \(\textsf {M}\) and let \(\uppi \,{:}\,{{\,\mathrm{\mathbf {G}}\,}}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\,{\ni }\,g\,{\rightarrow }\,g{\cdot }x\,{\in }\,\textsf {M}\) be the natural projection. The differential at x defines a map \(\uppi _{*}:\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\,{\rightarrow }\,\textsf {T}_{x}\textsf {M}\) of the Lie algebra \(\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) of \({{\,\mathrm{\mathbf {G}}\,}}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) onto the tangent space to \(\textsf {M}\) at x. By the formal integrability of the partial complex structure of \(\textsf {M},\) the pullback \(\mathfrak {q}\,{=}\,(\uppi ^{{{\,\mathrm{\mathbb {C}}\,}}}_{*})^{-1}(\textsf {T}^{0,1}_{x}\textsf {M})\) of the space of tangent vectors of type (0, 1) at x by the complexification of the differential is a complex Lie subalgebra \(\mathfrak {q}\) of the complexification \(\mathfrak {g}\,{=}\,{{\,\mathrm{\mathbb {C}}\,}}{\otimes }_{{{\,\mathrm{{\mathbb {R}}}\,}}}\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) of \(\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}}.\) Vice versa, the assignment of a complex Lie subalgebra \(\mathfrak {q}\) of \(\mathfrak {g}\) yields a formally integrable \({{\,\mathrm{\mathbf {G}}\,}}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\)-equivariant partial complex structure on a locally homogeneous space \(\textsf {M}\) of \({{\,\mathrm{\mathbf {G}}\,}}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) by the requirement that \(\textsf {T}_{x}^{0,1}\textsf {M}\,{=}\,\uppi ^{{{\,\mathrm{\mathbb {C}}\,}}}_{*}(\mathfrak {q})\) (see e.g. [1, 21]). These considerations led to the following definition.
Definition 1.1
A CR algebra is a pair \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q})\), consisting of a real Lie algebra \(\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) and a complex Lie subalgebra \(\mathfrak {q}\) of its complexification \(\mathfrak {g}{=}{{\,\mathrm{\mathbb {C}}\,}}{\otimes }_{{{\,\mathrm{{\mathbb {R}}}\,}}}\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\) such that the quotient \(\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}}/(\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\cap \mathfrak {q})\) is a finite dimensional real vector space.
We call the intersection \(\mathfrak {q}\cap \mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) its isotropy subalgebra and say that \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q})\) is effective when \(\mathfrak {q}\cap \mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) does not contain any nontrivial ideal of \(\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}}.\)
If \({{\,\mathrm{\mathbf {G}}\,}}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) is a real form of a complex Lie algebra \({{\,\mathrm{\mathbf {G}}\,}}\) and \(\mathfrak {q}\) the Lie algebra of its closed subgroup \(\mathbf {Q},\) then \(\textsf {M}\) is locally CR diffeomorphic to the orbit of \({{\,\mathrm{\mathbf {G}}\,}}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) in the complex homogeneous space \({{\,\mathrm{\mathbf {G}}\,}}{/}\mathbf {Q}\) and its CR structure is induced by the complex structure of \({{\,\mathrm{\mathbf {G}}\,}}{/}\mathbf {Q}.\) These considerations can be generalized to locally homogeneous CR manifolds (see e.g. [1]).
The CR-dimension and codimension of \(\textsf {M}\) are expressed in terms of its associated CR algebra \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q})\) by
Definition 1.3
We call fundamental a CR algebra \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q})\) such that \(\mathfrak {q}{+}{\bar{\mathfrak {q}}}\) generates \(\mathfrak {g}\) as a Lie algebra and we say that it is
-
of complex type if \(\mathfrak {q}{+}{\bar{\mathfrak {q}}}\,{=}\,\mathfrak {g},\)
-
of contact type if \(\mathfrak {q}{+}{\bar{\mathfrak {q}}}\,{\subsetneqq }\,\mathfrak {g}.\)
A corresponding CR manifold \(\textsf {M}\) is in the first case a complex manifold by Newlander-Nirenberg theorem (cf. [4, 22]), while contact type is equivalent to the fact that its CR distribution is strongly non-integrable.
2.3 Levi-order of weak nondegeneracy
The Levi form is a basic invariant of CR geometry. When \(\textsf {M}\) is locally homogeneous, it can be computed by using its associated CR algebra \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q})\) (for definitions and basic properties, cf. e.g. [9]). Nondegeneracy of the Levi form can be stated by
This is equivalent to
When this condition is not satisfied, we say that \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q})\) is Levi-degenerate. To measure the degeneracy of the Levi form, one can consider its iterations: in the homogeneous case this means, given a \(Z\,{\in }\,\mathfrak {q}{\backslash }(\mathfrak {q}{\cap }{\bar{\mathfrak {q}}}),\) to seek whether it is possible to find  such that
such that  To this aim, it is convenient to consider the descending chain (see e.g. [10, 12, 13, 18, 21])
To this aim, it is convenient to consider the descending chain (see e.g. [10, 12, 13, 18, 21])

Note that  for all integers
for all integers  Since by assumption \(\mathfrak {q}/(\mathfrak {q}{\cap }{\bar{\mathfrak {q}}})\) is finite dimensional, there is a smallest nonnegative integer
Since by assumption \(\mathfrak {q}/(\mathfrak {q}{\cap }{\bar{\mathfrak {q}}})\) is finite dimensional, there is a smallest nonnegative integer  such that
such that  for all
for all 
Definition 1.4
We call (1.11) the descending Levi chain of \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q}).\)
Let  be a positive integer. The CR algebra \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q})\) is said to be
be a positive integer. The CR algebra \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q})\) is said to be
-
weakly nondegenerate of Levi order
 if
if 
-
strictly nondegenerate if it is weakly nondegenerate of Levi order 1.
-
holomorphically degenerate if
 for all integers
for all integers 
Proposition 1.2
The terms \(\mathfrak {q}^{(p)}\) of (1.11) are Lie subalgebras of \(\mathfrak {q}.\)
Proof
By definition, \(\mathfrak {q}^{(0)}\,{=}\,\mathfrak {q}\) is a Lie subalgebra of \(\mathfrak {q}.\) If \(Z_{1},Z_{2}\,{\in }\,\mathfrak {q}^{(1)},\) then
because \([Z_{i},\mathfrak {q}]\,{\subseteq }\,[\mathfrak {q},\mathfrak {q}]\,{\subseteq }\,\mathfrak {q},\) and \([Z_{i},{\bar{\mathfrak {q}}}]\,{\subseteq }\,\mathfrak {q}{+}{\bar{\mathfrak {q}}}\) by the definition of \(\mathfrak {q}^{(1)}.\) This shows that \(\mathfrak {q}^{(1)}\) is a Lie subalgebra of \(\mathfrak {q}.\)
Next we argue by recurrence. Let  and assume that
and assume that  is a Lie subalgebra of \(\mathfrak {q}.\) If
is a Lie subalgebra of \(\mathfrak {q}.\) If  then
then  by the inductive assumption that
by the inductive assumption that  is a Lie subalgebra and
is a Lie subalgebra and

showing that also  This completes the proof. \(\square \)
This completes the proof. \(\square \)
Let us introduce the notation
The weak nondegeneracy defined here is equivalent to the notion of [21], consisting in the requirement that, for a complex Lie subalgebra \({{\,\mathrm{\mathfrak {f}}\,}}\) of \(\mathfrak {g},\)
Indeed, it easily follows from [21, Lemma 6.1] that

is the largest complex Lie subalgebra \({{\,\mathrm{\mathfrak {f}}\,}}\) of \(\mathfrak {g}\) with \(\mathfrak {q}\,{\subseteq }\,{{\,\mathrm{\mathfrak {f}}\,}}\,{\subseteq }\,{{\,\mathrm{\mathfrak {H}}\,}}.\)
2.4 Contact nondegeneracy
A less restrictive nondegeneracy condition in terms of iterations of the Levi form can be expressed by requiring that, given \(Z\,{\in }\,\mathfrak {q}{\backslash }(\mathfrak {q}{\cap }{\bar{\mathfrak {q}}})\) there are  such that
such that  For a CR algebra of the contact type this is equivalent to the fact that any ideal \({{\,\mathrm{\mathfrak {a}}\,}}\) of \(\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) that is contained in \({{\,\mathrm{\mathfrak {H}}\,}}_{\,{{\,\mathrm{{\mathbb {R}}}\,}}}\) is contained in \(\mathfrak {q}\,{\cap }\,\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}}.\) Thus this property was called ideal nondegeneracy in [21].
For a CR algebra of the contact type this is equivalent to the fact that any ideal \({{\,\mathrm{\mathfrak {a}}\,}}\) of \(\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) that is contained in \({{\,\mathrm{\mathfrak {H}}\,}}_{\,{{\,\mathrm{{\mathbb {R}}}\,}}}\) is contained in \(\mathfrak {q}\,{\cap }\,\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}}.\) Thus this property was called ideal nondegeneracy in [21].
When \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q})\) is the CR algebra at x of a (locally) homogeneous CR manifold \(\textsf {M},\) the subspace \({{\,\mathrm{\mathfrak {H}}\,}}_{\,{{\,\mathrm{{\mathbb {R}}}\,}}}\) is the pullback to \(\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) of the real contact distribution associated to the CR structure of \(\textsf {M}.\) Thus this notion was renamed contact nondegeneracy in [18]. It was shown in [21, Lemma 7.2] that, for the complexification \({{\,\mathrm{\mathfrak {a}}\,}}\) of the largest ideal of \(\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) contained in \({{\,\mathrm{\mathfrak {H}}\,}}_{\,{{\,\mathrm{{\mathbb {R}}}\,}}},\) the sum \({{\,\mathrm{\mathfrak {a}}\,}}{+}\mathfrak {q}\,{\cap }\,{\bar{\mathfrak {q}}}\) is the limit of the descending chain

Since  for all integers
for all integers  the chain (1.15) stabilizes.
the chain (1.15) stabilizes.
Remark 1.3
Note that, for 

This is true in fact for  and for
and for  follows from
follows from 
Definition 1.5
We call (1.15) the descending contact chain.
Let  be a positive integer. The CR algebra \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q})\) is said to have
be a positive integer. The CR algebra \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q})\) is said to have
-
finite contact order
 if
if 
If  for all integers
for all integers  we say that \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q})\) is contact degenerate.
we say that \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q})\) is contact degenerate.
We note that we can equivalently use the descending chain

of [21]. This follows from
Lemma 1.4
With the notation introduced above, we have:
-
1.
For each
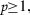
 is a Lie algebra and, for
is a Lie algebra and, for  an ideal of \({{\,\mathrm{\mathfrak {a}}\,}}_{{{\,\mathrm{{\mathbb {R}}}\,}}}^{(1)}\);
an ideal of \({{\,\mathrm{\mathfrak {a}}\,}}_{{{\,\mathrm{{\mathbb {R}}}\,}}}^{(1)}\); -
2.
Let
 be the complexification of
be the complexification of  Then
Then 
Proof
The first statement is trivial. We can check the second one by recurrence. This is in fact true for  since \(\mathfrak {q}{+}{\bar{\mathfrak {q}}}\) is the complexification of \({{\,\mathrm{\mathfrak {H}}\,}}.\) \(\square \)
since \(\mathfrak {q}{+}{\bar{\mathfrak {q}}}\) is the complexification of \({{\,\mathrm{\mathfrak {H}}\,}}.\) \(\square \)
We already considered two descending chains whose length defines the order of contact nondegeneracy. It is in fact convenient to consider a third one, which is easier to deal with (see Sect. 2 below), namely:

The equivalence is a consequence of
Proposition 1.5
With the notation above:
-
 for all integers
for all integers 
-
\((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q})\) is contact nondegenerate of order
 if and only if
if and only if 
\(\square \)
Since we obviously have the inclusion

we obtain
Proposition 1.6
If the CR algebra \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q})\) has Levi order  then \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q})\) has contact order
then \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q})\) has contact order  A contact degenerate \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q})\) is also holomorphically degenerate. \(\square \)
A contact degenerate \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q})\) is also holomorphically degenerate. \(\square \)
3 Orbits of real forms in complex flag manifolds
3.1 Complex flag manifolds
A complex flag manifold \(\textsf {F}\) is a smooth compact algebraic variety that can be described as the quotient of a complex semisimple Lie group \(\mathbf {S}\) by a parabolic subgroup \(\mathbf {Q}\); according to Wolf [27], a real form \(\mathbf {S}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) of \(\mathbf {S}\) has finitely many orbits in \(\textsf {F}.\) Only one of them, having minimal dimension, is compact. With the partial complex structures induced by \(\textsf {F},\) these orbits make a class of homogeneous CR manifolds that were studied by many authors (see e.g. [1,2,3, 8, 10, 11, 14, 17, 19]).
Cross-marked Dynkin diagrams Being connected and simply connected, a complex flag manifold \(\textsf {F}\,{=}\,\mathbf {S}/\mathbf {Q}\) is completely described by the Lie pair \(({{\,\mathrm{\mathfrak {s}}\,}},\mathfrak {q})\) consisting of the Lie algebras of \(\mathbf {S}\) and of \(\mathbf {Q}\) and vice versa to any Lie pair \(({{\,\mathrm{\mathfrak {s}}\,}},\mathfrak {q})\) of a complex semisimple Lie algebra and its parabolic subalgebra \(\mathfrak {q}\) corresponds a unique flag manifold \(\textsf {F}.\) Therefore the classification of complex flag manifolds reduces to that of parabolic subalgebras of semisimple complex Lie algebras. Parabolic subalgebras \(\mathfrak {q}\) of \({{\,\mathrm{\mathfrak {s}}\,}}\) are classified, modulo automorphisms, by a finite set of parameters. In fact, after fixing any Cartan subalgebra \(\mathfrak {h}\) of \({{\,\mathrm{\mathfrak {s}}\,}},\) their equivalence classes are in one to one correspondence with the subsets of a basis  of simple roots of the root system
of simple roots of the root system  of \(({{\,\mathrm{\mathfrak {s}}\,}},\mathfrak {h})\) (see e.g. [7, Ch.VIII,§3.4]).
of \(({{\,\mathrm{\mathfrak {s}}\,}},\mathfrak {h})\) (see e.g. [7, Ch.VIII,§3.4]).
We recall that the Dynkin diagram  is a graph with no loops, whose nodes are the roots in
is a graph with no loops, whose nodes are the roots in  and in which two nodes may be joined by at most 3 edges. Each root \(\upbeta \) in
and in which two nodes may be joined by at most 3 edges. Each root \(\upbeta \) in  can be written in a unique way as a nontrivial linear combination
can be written in a unique way as a nontrivial linear combination

with integral coefficients \(k_{\upbeta ,\upalpha }\) which are either all \(\ge {0},\) or all \(\le {0}\) and we set

The parabolic subalgebras \(\mathfrak {q}\) are parametrized, modulo isomorphisms, by subsets \(\Phi \) of  : to a
: to a  we associate
we associate

The set \(\texttt {Q}_{\Phi }\) is a parabolic set of roots, i.e.

To specify the \(\mathfrak {q}_{\Phi }\) of (2.3) we can cross the nodes corresponding to the roots in \(\Phi .\) In this way each cross-marked Dynkin diagram encodes a specific complex flag manifold \(\textsf {F}_{\Phi }.\)
Notation 2.1
Let \(\upxi _{\Phi }\) be the linear functional on the linear span of  which equals one on the roots in \(\Phi \) and zero on those in
which equals one on the roots in \(\Phi \) and zero on those in  Then
Then

and we get partitions

We recall (see e.g. [7, Ch.VIII,§3]):
-
\(\mathfrak {q}^{r}_{\Phi }=\mathfrak {h}\oplus {\sum }_{\upbeta \in \texttt {Q}^{r}_{\Phi }}{{\,\mathrm{\mathfrak {s}}\,}}^{\upbeta }\) is a reductive complex Lie algebra;
-
\(\mathfrak {q}^{n}_{\Phi }={\sum }_{\upbeta \in \texttt {Q}^{n}_{\Phi }}{{\,\mathrm{\mathfrak {s}}\,}}^{\upbeta }\) is the nilradical of \(\mathfrak {q}_{\Phi }\);
-
\(\mathfrak {q}_{\Phi }=\mathfrak {q}^{r}_{\Phi }\oplus \mathfrak {q}^{n}_{\Phi }\) is the Levi-Chevalley decomposition of \(\mathfrak {q}_{\Phi }\);
-
\(\mathfrak {q}_{\Phi }^{c}={\sum }_{\upbeta \in \texttt {Q}^{c}_{\Phi }}{{\,\mathrm{\mathfrak {s}}\,}}^{\upbeta }\) is a Lie subalgebra of \({{\,\mathrm{\mathfrak {s}}\,}}\) consisting of \({{\,\mathrm{\mathrm {ad}}\,}}_{{{\,\mathrm{\mathfrak {s}}\,}}}\)-nilpotent elements;
-
\(\mathfrak {q}^{\vee }_{\Phi }=\mathfrak {q}^{r}_{\Phi }\oplus \mathfrak {q}^{c}_{\Phi }\) is the parabolic Lie subalgebra of \({{\,\mathrm{\mathfrak {s}}\,}}\) opposite of \(\mathfrak {q}_{\Phi }\), decomposed into the direct sum of its reductive subalgebra \(\mathfrak {q}^{r}_{\Phi }\) and its nilradical \(\mathfrak {q}^{c}_{\Phi }.\)
3.2 Real forms
Let us take, as we can, \(\mathbf {S}\) connected and simply connected. Then real automorphisms of its Lie algebra \({{\,\mathrm{\mathfrak {s}}\,}}\) lift to automorphisms of the Lie group \(\mathbf {S},\) so that real forms \(\mathbf {S}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) of \(\mathbf {S}\) are in one-to-one correspondence with the anti-\({{\,\mathrm{\mathbb {C}}\,}}\)-linear involutions \(\upsigma \) of \({{\,\mathrm{\mathfrak {s}}\,}}.\) We will denote by \({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma }\) the real Lie subalgebra consisting of the fixed points of \(\upsigma \): it is the Lie algebra of the real form \(\mathbf {S}_{\upsigma }\) of fixed points of the lift \({\tilde{\upsigma }}\) of \(\upsigma \) to \(\mathbf {S}.\) Its orbits are CR submanifolds \(\textsf {M}_{\Phi ,\upsigma }\) of \(\textsf {F}_{\Phi }\) whose CR algebra at the base point \(\mathbf {Q}\) is the pair \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi }).\)
Definition 2.1
(cf. [1, §5]) A parabolic CR algebra is a pair \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) consisting of a real semisimple Lie algebra \({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma }\) and a parabolic complex Lie subalgebra \(\mathfrak {q}_{\Phi }\) of its complexification \({{\,\mathrm{\mathfrak {s}}\,}}.\) We say that \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is minimal if \(\textsf {M}_{\Phi ,\upsigma }\) is the minimal orbit in \(\textsf {F}_{\Phi }\) of the real form \(\mathbf {S}_{\upsigma }\) of \(\mathbf {S}.\)
When \({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma }\) is not simple, the corresponding orbits \(\textsf {M}_{\Phi ,\upsigma }\) are CR diffeomorphic to a cartesian product of orbits of simple real Lie groups (see e.g. [3]).If
we call each \(\textsf {M}_{\Phi _{i},\upsigma _{i}}\) a factor of \(\textsf {M}_{\Phi ,\upsigma }.\)
A simple \({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma }\) is of the real type if also \({{\,\mathrm{\mathfrak {s}}\,}}\) is simple; otherwise, \({{\,\mathrm{\mathfrak {s}}\,}}\) is the direct sum of two complex simple Lie algebras \({{\,\mathrm{\mathfrak {s}}\,}}',{{\,\mathrm{\mathfrak {s}}\,}}''\), which are \({{\,\mathrm{{\mathbb {R}}}\,}}\)-isomorphic to \({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\) and we say in this case that \({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma }\) is of the complex type.
To list all the orbits of a real form, one can use the fact that the isotropy subalgebra \({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma }{\cap }\,\mathfrak {q}\) contains a Cartan subalgebra \(\mathfrak {h}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) of \({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma }\) (see e.g. [3]). By choosing \(\mathfrak {h}\) equal to its complexification, we obtain on  a conjugation which is compatible with the one defined on \({{\,\mathrm{\mathfrak {s}}\,}}\) by its real form \({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma }\) (and which, for simplicity, we still denote by \(\upsigma \)). Vice versa, an orthogonal involution \(\upsigma \) of
a conjugation which is compatible with the one defined on \({{\,\mathrm{\mathfrak {s}}\,}}\) by its real form \({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma }\) (and which, for simplicity, we still denote by \(\upsigma \)). Vice versa, an orthogonal involution \(\upsigma \) of  lifts, although in general not in a unique way, to a conjugation of \({{\,\mathrm{\mathfrak {s}}\,}}\). The conjugation on \({{\,\mathrm{\mathfrak {s}}\,}}\) depends indeed also on the description of which roots in
lifts, although in general not in a unique way, to a conjugation of \({{\,\mathrm{\mathfrak {s}}\,}}\). The conjugation on \({{\,\mathrm{\mathfrak {s}}\,}}\) depends indeed also on the description of which roots in  are compact. This is determined by the choice of a Cartan involution \(\uptheta \) on \({{\,\mathrm{\mathfrak {s}}\,}},\) with \(\uptheta (\mathfrak {h})\,{=}\,\mathfrak {h}\) and \(\upsigma {\circ }\uptheta \,{=}\,\uptheta {\circ } \upsigma \), which induces a map, that we will denote by the same symbol,
are compact. This is determined by the choice of a Cartan involution \(\uptheta \) on \({{\,\mathrm{\mathfrak {s}}\,}},\) with \(\uptheta (\mathfrak {h})\,{=}\,\mathfrak {h}\) and \(\upsigma {\circ }\uptheta \,{=}\,\uptheta {\circ } \upsigma \), which induces a map, that we will denote by the same symbol,

We will write for simplicity \({\bar{\upalpha }}\) instead of \(\upsigma (\upalpha )\) and  for
for  when this will not cause confusion. We recall that \({{\,\mathrm{{\upkappa }}\,}}_{\upsigma }\,{=}\,\{X\,{\in }\,{{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma }\,{\mid }\,\uptheta (X){=}X\}\) is a maximal compact Lie subalgebra of \({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma }\) and that we have the Cartan decomposition
when this will not cause confusion. We recall that \({{\,\mathrm{{\upkappa }}\,}}_{\upsigma }\,{=}\,\{X\,{\in }\,{{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma }\,{\mid }\,\uptheta (X){=}X\}\) is a maximal compact Lie subalgebra of \({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma }\) and that we have the Cartan decomposition
of \({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma }\). When \(\uptheta (\upalpha )\,{=}\upalpha ,\) then either \({{\,\mathrm{\mathfrak {s}}\,}}^{\upalpha }\) is contained in the complexification \({{\,\mathrm{{\upkappa }}\,}}\) of \({{\,\mathrm{{\upkappa }}\,}}_{\upsigma }\) (compact root) or in the complexification \({{\,\mathrm{\mathfrak {p}}\,}}\) of \({{\,\mathrm{\mathfrak {p}}\,}}_{\upsigma }\) (hermitian root).
The subalgebras \(\mathfrak {q}_{\Phi }\,{\cap }\,{\bar{\mathfrak {q}}}_{\Phi },\) \(\mathfrak {q}_{\Phi }\) and \({\bar{\mathfrak {q}}}_{\Phi }\) turn out to be direct sums of \(\mathfrak {h}\) and root subspaces \({{\,\mathrm{\mathfrak {s}}\,}}^{\upalpha }\); in particular \(\mathfrak {q}_{\Phi }\,{\cap }\,{\bar{\mathfrak {q}}}_{\Phi }\) is the direct sum of \(\mathfrak {h}\) and the root subspaces \({{\,\mathrm{\mathfrak {s}}\,}}^{\upalpha }\) with \({{\,\mathrm{\mathfrak {s}}\,}}^{\upalpha }{+}{{\,\mathrm{\mathfrak {s}}\,}}^{{\bar{\upalpha }}}\,{\subset }\,\mathfrak {q}_{\Phi }.\)
We note that \(\mathfrak {q}_{\Phi }\,{\cap }\,{\bar{\mathfrak {q}}}_{\Phi }\) is a Lie subalgebra of \({{\,\mathrm{\mathfrak {s}}\,}}\) and \((\mathfrak {q}_{\Phi }\,{+}\,{\bar{\mathfrak {q}}}_{\Phi })\) is a \((\mathfrak {q}_{\Phi }\,{\cap }\,{\bar{\mathfrak {q}}}_{\Phi })\)-module.
Having fixed a base  of simple roots of the root system
of simple roots of the root system  associated to \(({{\,\mathrm{\mathfrak {s}}\,}},\mathfrak {h}),\) the orbit of the real form is determined by the data of:
associated to \(({{\,\mathrm{\mathfrak {s}}\,}},\mathfrak {h}),\) the orbit of the real form is determined by the data of:
-
a subset \(\Phi \) of
 specifying the parabolic subalgebra \(\mathfrak {q}_{\Phi }\);
specifying the parabolic subalgebra \(\mathfrak {q}_{\Phi }\); -
a conjugation \(\upsigma \) of
 ;
; -
a splitting
 of
of 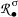 into a first set consisting of the compact and a second of the hermitian roots.
into a first set consisting of the compact and a second of the hermitian roots.
We point out that different choices of \(\upsigma \) may yield the same CR submanifold \(\textsf {M}_{\Phi ,\upsigma }.\) In particular, we can conjugate \(\upsigma \) by any element of the subgroup of the Weyl group generated by reflections with respect to roots in 
3.3 Contact nondegeneracy for parabolic CR algebras
Since by definition simple Lie algebra have no proper nontrivial ideals, we obtain
Proposition 2.1
A real orbit \(\textsf {M}_{\Phi ,\upsigma }\) which is fundamental and does not have a totally complex factor is contact nondegenerate.
Proof
We can indeed reduce to the case where \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is effective and \({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma }\) is simple, in which the proof is straightforward. \(\square \)
We have the following criterion
Proposition 2.2
A real orbit \(\textsf {M}_{\Phi ,\upsigma }\) is fundamental iff its CR algebra \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is fundamental.
Let \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) be a parabolic CR algebra and set
If \(\Phi ^{\upsigma }_{\circ }\,{=}\,\emptyset ,\) then \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is fundamental. When \(\Phi ^{\upsigma }_{\circ }\,{\ne }\,\emptyset ,\) we have
-
\(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is fundamental if and only if \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi ^{\upsigma }_{\circ }})\) is fundamental;
-
\(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) and \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi ^{\upsigma }_{\circ }})\) are fundamental if and only if
$$\begin{aligned} {\bar{\texttt {Q}}}_{\Phi ^{\upsigma }_{\circ }}^{\, c}\cap \Phi ^{\upsigma }_{\circ }=\emptyset . \end{aligned}$$(2.8)
Proof
If \(\Phi ^{\upsigma }_{\circ }\,{=}\,\emptyset ,\) then  and hence \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is trivially fundamental. Let us consider next the case where \(\Phi ^{\upsigma }_{\circ }\,{\ne }\,\emptyset .\)
and hence \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is trivially fundamental. Let us consider next the case where \(\Phi ^{\upsigma }_{\circ }\,{\ne }\,\emptyset .\)
Since \(\Phi ^{\upsigma }_{\circ }\,{\subseteq }\,\Phi ,\) we have \(\mathfrak {q}_{\Phi }\,{\subseteq }\,\mathfrak {q}_{\Phi ^{\upsigma }_{\circ }}\) and therefore \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi ^{\upsigma }_{\circ }})\) is fundamental when \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is fundamental. To show the vice versa, we note that any Lie subalgebra of \({{\,\mathrm{\mathfrak {s}}\,}}\) containing \(\mathfrak {q}_{\Phi }\) is of the form \(\mathfrak {q}_{\Psi }\) for some \(\Psi \,{\subseteq }\,\Phi .\) If it contains \(\mathfrak {q}_{\Phi }{+}{\bar{\mathfrak {q}}}_{\Phi },\) then \(\Psi \,{\subseteq }\,\Phi ^{\upsigma }_{\circ }.\) This proves the first item.
It suffices to prove the second item in the case where \(\Phi \,{=}\,\Phi ^{\upsigma }_{\circ }.\) Then condition (2.8) is equivalent to the fact that each  belongs either to \(\texttt {Q}_{\Phi }\) or to \({\bar{\texttt {Q}}}_{\Phi }\) and is therefore clearly sufficient for \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) being fundamental. Vice versa, when this condition is not satisfied, we can pick \(\upalpha \,{\in }\, {\bar{\texttt {Q}}}^{\,c}_{\Phi }{\cap }\Phi .\) Then \(\mathfrak {q}_{\{\upalpha \}}\) is a proper parabolic subalgebra of \({{\,\mathrm{\mathfrak {s}}\,}}\) containing both \(\mathfrak {q}_{\Phi }\) and \({\bar{\mathfrak {q}}}_{\Phi }.\) Therefore \(\mathfrak {q}_{\Phi }{+}\,{\bar{\mathfrak {q}}}_{\Phi }\) generates a proper Lie subalgebra of \({{\,\mathrm{\mathfrak {s}}\,}}\) and hence \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is not fundamental. This completes the proof. \(\square \)
belongs either to \(\texttt {Q}_{\Phi }\) or to \({\bar{\texttt {Q}}}_{\Phi }\) and is therefore clearly sufficient for \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) being fundamental. Vice versa, when this condition is not satisfied, we can pick \(\upalpha \,{\in }\, {\bar{\texttt {Q}}}^{\,c}_{\Phi }{\cap }\Phi .\) Then \(\mathfrak {q}_{\{\upalpha \}}\) is a proper parabolic subalgebra of \({{\,\mathrm{\mathfrak {s}}\,}}\) containing both \(\mathfrak {q}_{\Phi }\) and \({\bar{\mathfrak {q}}}_{\Phi }.\) Therefore \(\mathfrak {q}_{\Phi }{+}\,{\bar{\mathfrak {q}}}_{\Phi }\) generates a proper Lie subalgebra of \({{\,\mathrm{\mathfrak {s}}\,}}\) and hence \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is not fundamental. This completes the proof. \(\square \)
Example 2.3
Fix \(n{\ge }3.\) The cross-marked Dynkin diagram

describes the flag manifold \(\textsf {F}_{\Phi }\) of \(\mathbf {SL}_{n+1}({{\,\mathrm{\mathbb {C}}\,}})\) consisting of flags
where \(\ell _{d}\) is a d-dimensional linear subspace of \({{\,\mathrm{\mathbb {C}}\,}}^{n+1}.\) Here

We consider the conjugation \(\upsigma \) defined by
Then \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is contact nondegenerate of order \([(n{-}1)/2].\) It is weakly nondegenerate for \(n\,{=}\,3,4\) and holomorphically degenerate for \(n{\ge }5.\)
3.4 Conditions for weak nondegeneracy
To discuss weak nondegeneracy, we observe that the terms of the chain (1.11) for \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) can be described by the combinatorics of the root system. We recall that the chain is

Each  in the chain is the direct sum of \(\mathfrak {h}\) and root spaces \({{\,\mathrm{\mathfrak {s}}\,}}^{\upalpha }.\) Let us set
in the chain is the direct sum of \(\mathfrak {h}\) and root spaces \({{\,\mathrm{\mathfrak {s}}\,}}^{\upalpha }.\) Let us set

With the notation of Sect. 2.1, we have \(\texttt {Q}_{\Phi }^{0}=\texttt {Q}_{\Phi }\) and

This yields a characterization of weak nondegeneracy in terms of roots:
Proposition 2.4
A necessary and sufficient condition for \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) being weakly nondegenerate of Levi order  is that
is that  \(\square \)
\(\square \)
Remark 2.5
The necessary and sufficient condition for \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) being weakly nondegenerate is that (cf. [1, Lemma 12.1])

Definition 2.2
For any root \(\upbeta \,{\in }\,\texttt {Q}_{\Phi }{\backslash }{\bar{\texttt {Q}}}_{\Phi }\) we denote by  and call its Levi order the smallest number k for which (2.11) is valid. We put
and call its Levi order the smallest number k for which (2.11) is valid. We put  when (2.11) is not valid for any positive integer k.
when (2.11) is not valid for any positive integer k.
Lemma 2.6
Assume that \(\upbeta \,{\in }\,\texttt {Q}_{\Phi }{\backslash }{\bar{\texttt {Q}}}_{\Phi }\) has finite Levi order  and (2.11) is satisfied for a sequence
and (2.11) is satisfied for a sequence  Then
Then
-
(i)
\(\upalpha _{i}\in {\bar{\texttt {Q}}}_{\Phi }{\backslash }\texttt {Q}_{\Phi }\) for all
 ;
; -
(ii)
\(\upbeta +{\sum }_{i{\le }h}{\upalpha _{i}}\in \texttt {Q}_{\Phi }{\backslash }{\bar{\texttt {Q}}}_{\Phi }\) for all
 ;
; -
(iii)
(2.11) is satisfied by all permutations of
 ;
; -
(iv)
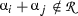 for all
for all 
Proof
Let us first prove (ii). With the notation in (2.11), we observe that \(\upgamma _{h}\,{\notin }\,{\bar{\texttt {Q}}}_{\Phi }\) for  because, otherwise,
because, otherwise, 
Next we prove (iii). Let  be a Chevalley basis for \(({{\,\mathrm{\mathfrak {s}}\,}},\mathfrak {h}).\) Then (2.11) is equivalent to the fact that
be a Chevalley basis for \(({{\,\mathrm{\mathfrak {s}}\,}},\mathfrak {h}).\) Then (2.11) is equivalent to the fact that

The item (iii) follows because

and, by the minimality assumption, the right hand side belongs to \(\mathfrak {q}_{\Phi }{+}{\bar{\mathfrak {q}}}_{\Phi }.\)
Let us prove (i) by contradiction. If \(\upalpha _{i}\,{\in }\,\texttt {Q}_{\Phi }\,{\cap }\,{\bar{\texttt {Q}}}_{\Phi }\) for some  then we could assume by (iii) that it was
then we could assume by (iii) that it was  Then
Then

yields the contradiction. Also (iv) is an easy consequence of (iii), because if \(\upalpha _{i}{+}\upalpha _{j}\) ( ) is a root, than it would belong to \({\bar{\texttt {Q}}}_{\Phi }\,{\cap }\, \texttt {Q}_{\Phi }^{c}\) and, by substituting to the two roots \(\upalpha _{i},\;\upalpha _{j}\) the single root \(\upalpha _{i}{+}\upalpha _{j}\) we would obtain a sequence satisfying (2.11) and containing
) is a root, than it would belong to \({\bar{\texttt {Q}}}_{\Phi }\,{\cap }\, \texttt {Q}_{\Phi }^{c}\) and, by substituting to the two roots \(\upalpha _{i},\;\upalpha _{j}\) the single root \(\upalpha _{i}{+}\upalpha _{j}\) we would obtain a sequence satisfying (2.11) and containing  terms.
terms.
The proof is complete. \(\square \)
Remark 2.7
Since \(\upxi _{\Phi }(\upalpha ){\ge }1\) for all \(\upalpha \,{\in }\texttt {Q}^{\,c}_{\Phi },\) if \(\upbeta \,{\in }\,\texttt {Q}_{\Phi }\,{\cap }\,{\bar{\texttt {Q}}}^{\,c}_{\Phi }\) and  then
then

Corollary 2.8
If \(\upbeta \,{\in }\, \texttt {Q}^{\,r}_{\Phi }{\backslash }{\bar{\texttt {Q}}}_{\Phi },\) then its Levi order is either one or \({+}\infty .\) \(\square \)
We obtain also a useful criterion of weak nondegeneracy (cf. [3, Thm.6.4])
Proposition 2.9
The parabolic CR algebra \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is weakly nondegenerate if and only if
Proof
By Lemma 2.6 the condition is necessary. To prove that it is also sufficient, we can argue by contradiction: if we could find \(\upbeta \,{\in }\,\texttt {Q}\,{\cap }\,{\bar{\texttt {Q}}}^{\,c}_{\Phi }\) with  then by (2.13) we could construct an infinite sequence \((\upalpha _{i})_{i\ge {1}}\) in \({\bar{\texttt {Q}}}_{\Phi }\,{\cap }\,\texttt {Q}_{\Phi }^{\,c}\) with
then by (2.13) we could construct an infinite sequence \((\upalpha _{i})_{i\ge {1}}\) in \({\bar{\texttt {Q}}}_{\Phi }\,{\cap }\,\texttt {Q}_{\Phi }^{\,c}\) with
Since \(\upxi _{\Phi }(\upgamma _{h})\ge \upxi _{\Phi }(\upbeta ){+}h\) and \(\upxi _{\Phi }\) is bounded, we get a contradiction. \(\square \)
3.5 Levi order of general orbits
To discuss Levi order of weakly nondegenerate real orbits \(\textsf {M}_{\Phi ,\upsigma }\) in \(\textsf {F}_{\Phi }\) by employing Lemma 2.6, we introduce:
Definition 2.3
If  we denote by
we denote by  the largest positive integer
the largest positive integer  for which
for which

Proposition 2.10
Let  belong to a simple root system containing more than two elements. Then
belong to a simple root system containing more than two elements. Then  and, if
and, if  and \((\upalpha _{1},\upalpha _{2},\upalpha _{3},\upalpha _{4})\) is a sequence satisfying (2.14), then
and \((\upalpha _{1},\upalpha _{2},\upalpha _{3},\upalpha _{4})\) is a sequence satisfying (2.14), then
More precisely we obtain:

Proof
For short we will call admissible a sequence \((\upalpha _{i})\) for which (2.14) is valid. Let us set

We consider the different cases using for root systems the notation of [6].
Type \(\mathrm {A}\) We have  where \(e_{1},\hdots ,e_{n}\) is an orthonormal basis of \({{\,\mathrm{{\mathbb {R}}}\,}}^{n}.\) We can take \(\upbeta =e_{2}{-}e_{1}.\) Then
where \(e_{1},\hdots ,e_{n}\) is an orthonormal basis of \({{\,\mathrm{{\mathbb {R}}}\,}}^{n}.\) We can take \(\upbeta =e_{2}{-}e_{1}.\) Then

An admissible sequence \((\upalpha _{i})\) can contain at most one element from each of the two sets in the right hand side of \((*A).\)
If \(n\,{=}\,3,\) then  contains two elements, whose sum is still a root and therefore
contains two elements, whose sum is still a root and therefore 
If \(n{>}3,\) then the only possible choice is that of a couple of roots \(e_{i}{-}e_{2},\, e_{1}{-}e_{j}\) with \(3\,{\le }i{\ne }j{\le }n\) and hence 
Type \(\mathrm {B}\) We have  for an orthonormal basis \(e_{1},\hdots ,e_{n}\) of \({{\,\mathrm{{\mathbb {R}}}\,}}^{n}\) (\(n{\ge }2\)).
for an orthonormal basis \(e_{1},\hdots ,e_{n}\) of \({{\,\mathrm{{\mathbb {R}}}\,}}^{n}\) (\(n{\ge }2\)).
If \(\upbeta \) is a short root, we can take \(\upbeta \,{=}\,{-}e_{1}.\) Then

An admissible sequence contains at most one root from the first and two from the second set in the right hand side of \((*B).\) Thus  The sequence \(e_{1}{-}e_{2},\,e_{1}{+}e_{2}\) satisfies (2.14) and therefore
The sequence \(e_{1}{-}e_{2},\,e_{1}{+}e_{2}\) satisfies (2.14) and therefore 
We have equality if \(n{=}2,\) because in this case  and the maximal admissible sequences are then \((e_{2}),\) \(({-}e_{2}),\) \((e_{1}{+}e_{2},\, e_{1}{-}e_{2}).\)
and the maximal admissible sequences are then \((e_{2}),\) \(({-}e_{2}),\) \((e_{1}{+}e_{2},\, e_{1}{-}e_{2}).\)
If \(n{>}2\) the admissible sequence
shows that  All admissible maximal sequences are of this form.
All admissible maximal sequences are of this form.
If \(\upbeta \) is a long root, we can assume that \(\upbeta \,{=}\,-e_{1}{-}e_{2}.\) Then

An admissible sequence contains at most two equal terms from the first and two from each of the second and third on the right hand side of \(({*\!*\!{B}}).\) Moreover, if one term is taken from the first, we can take at most one from each one of the other two. This implies that  and in fact
and in fact  with maximal sequences isomorphic to one of
with maximal sequences isomorphic to one of

which, summed up to \(({-}e_{1}{-}e_{2}),\) gives \(e_{1}{+}e_{2}.\)
Type \(\mathrm {C}\) We can take  for an orthonormal basis \(e_{1},\hdots ,e_{n}\) of \({{\,\mathrm{{\mathbb {R}}}\,}}^{n}\) (\(n{\ge }3\)).
for an orthonormal basis \(e_{1},\hdots ,e_{n}\) of \({{\,\mathrm{{\mathbb {R}}}\,}}^{n}\) (\(n{\ge }3\)).
If \(\upbeta \) is a short root, we can assume that \(\upbeta {=}({-}e_{1}{-}e_{2}).\) Then

An admissible sequence may contain both roots of the first, but at most one root from each the second and third sets on the right hand side of \((*C).\) Moreover, a term in one of the last two forbids the corresponding term in the first one. This yields  with maximal sequences isomorphic to (the third one should be omitted if \(n{=}3\))
with maximal sequences isomorphic to (the third one should be omitted if \(n{=}3\))
If \(\upbeta \) is a long root, we can assume that \(\upbeta \,{=}\,{-}2e_{1}.\) Then

We note that  We cannot take in an admissible sequence both the element \(e_{1}{+}e_{i}\) and \(e_{1}{-}e_{i},\) because they add up to the root \(2e_{i}.\) Hence in fact
We cannot take in an admissible sequence both the element \(e_{1}{+}e_{i}\) and \(e_{1}{-}e_{i},\) because they add up to the root \(2e_{i}.\) Hence in fact  with maximal sequence isomorphic to
with maximal sequence isomorphic to
Type \(\mathrm {D}\) We can take  where \(e_{1},\hdots ,e_{n}\) is an orthonormal basis of \({{\,\mathrm{{\mathbb {R}}}\,}}^{n}\) (\(n{\ge }4\)).
where \(e_{1},\hdots ,e_{n}\) is an orthonormal basis of \({{\,\mathrm{{\mathbb {R}}}\,}}^{n}\) (\(n{\ge }4\)).
We can assume that \(\upbeta ={-}e_{1}{-}e_{2}.\) We have

An admissible sequence contains at most two elements from each set in the right hand side of \((*D).\) Therefore  and in fact we have equality with maximal admissible sequences isomorphic to
and in fact we have equality with maximal admissible sequences isomorphic to
which, summed up to \(({-}e_{1}{-}e_{2}),\) give \(e_{1}{+}e_{2}.\)
Type \(\mathrm {E}\) Since the root systems \(\mathrm {E}_{6}\) and \(\mathrm {E}_{7}\) can be considered as subsystems of \(\mathrm {E}_{8},\) we will restrain to this case. We consider, for an orthonormal basis \(e_{1},\hdots ,e_{8}\) of \({{\,\mathrm{{\mathbb {R}}}\,}}^{8},\)

We can take \(\upbeta \,{=}\,({-}e_{1}{-}e_{2}).\) Then

An admissible sequence may contain at most two roots from each set on the right hand side of \((*E)\) and no more than four terms. Clearly we can take the maximal sequence
showing that  Moreover, any admissible sequence containing four terms sums up to \(({-}e_{1}{-}e_{2})\) to yield \(e_{1}{+}e_{2}.\)
Moreover, any admissible sequence containing four terms sums up to \(({-}e_{1}{-}e_{2})\) to yield \(e_{1}{+}e_{2}.\)
Type \(\mathrm {F}\) For an orthonormal basis \(e_{1},e_{2},e_{3},e_{4}\) of \({{\,\mathrm{{\mathbb {R}}}\,}}^{4}\) we take

If \(\upbeta \) is a short root, we can take \(\upbeta {=}{-}e_{1}.\) Then

To build an an admissible sequence we can take at most one element from the first, two from the second and from the third set in the right hand side of \((*F).\) Indeed two roots of the form \(\tfrac{1}{2}({\pm }e_{1}{\pm }e_{2}{\pm }e_{3}{\pm }e_{4})\) do not add up to a root if and only if they differ by only one sign. Moreover, no root can be taken from the first if one is taken from the last set. These considerations imply that  and in fact equality holds, as \(({-}e_{1})\) is contained in a subsystem of type \(\mathrm {B}_{3}.\)
and in fact equality holds, as \(({-}e_{1})\) is contained in a subsystem of type \(\mathrm {B}_{3}.\)
If \(\upbeta \) is a long root, we can assume \(\upbeta {=}({-}e_{1}{-}e_{2}).\) We have

We note that the sum of four terms of  is a linear combination \(\upbeta +k_{1}e_{1}{+}k_{2}e_{2}{+}k_{3}e_{3}{+}k_{4}e_{4}\) with \(k_{1}{+}k_{2}{\ge }2\) and therefore, if they form an admissible sequence, is equal to \(e_{1}{+}e_{2}.\) Since
is a linear combination \(\upbeta +k_{1}e_{1}{+}k_{2}e_{2}{+}k_{3}e_{3}{+}k_{4}e_{4}\) with \(k_{1}{+}k_{2}{\ge }2\) and therefore, if they form an admissible sequence, is equal to \(e_{1}{+}e_{2}.\) Since  contains subsystems of type \(\mathrm {B}_{3},\) there are indeed admissible sequences with four elements.
contains subsystems of type \(\mathrm {B}_{3},\) there are indeed admissible sequences with four elements.
Type \(\mathrm {G}\) For an orthonormal basis \(e_{1},e_{2},e_{3}\) of \({{\,\mathrm{{\mathbb {R}}}\,}}^{3}\) we set

We consider firs the case of a short root. We can take \(\upbeta =e_{2}{-}e_{1}.\) Then

Maximal admissible sequences have a root from the first and one from the second set, hence  and, moreover, summed up to \(e_{2}{-}e_{1},\) give \(e_{1}{-}e_{2}.\)
and, moreover, summed up to \(e_{2}{-}e_{1},\) give \(e_{1}{-}e_{2}.\)
As a long root we take \(\upbeta =(e_{2}{+}e_{3}{-}2e_{1}).\) Then

One checks that in this case  with a maximal admissible sequence
with a maximal admissible sequence
which indeed sums up to the opposite root \(2e_{1}{-}e_{2}{-}e_{3}.\)
The proof is complete. \(\square \)
As an easy consequence we obtain:
Theorem 2.11
Let \(\textsf {M}_{\Phi ,\upsigma }\) be a real orbit which is fundamental and weakly nondegenerate. Then its Levi order is less or equal to 3.
Proof
This is a consequence of Prop.2.10 and the fact that, if \(\upbeta \) does not belong to \({\bar{\texttt {Q}}}_{\Phi },\) then \({-}\upbeta \in {\bar{\texttt {Q}}}_{\Phi }\) because \({\bar{\texttt {Q}}}_{\Phi }\) is a parabolic set of roots. \(\square \)
Example 2.12
([10, §7]) Let n be an integer \(\ge {3}\) and fix a symmetric \({{\,\mathrm{\mathbb {C}}\,}}\)-bilinear form \(\mathfrak {b}\) on \({{\,\mathrm{\mathbb {C}}\,}}^{2n+1}\! .\) The Lie algebra of the group of \({{\,\mathrm{\mathbb {C}}\,}}\)-linear transformations of \({{\,\mathrm{\mathbb {C}}\,}}^{2n+1}\) that keep \(\mathfrak {b}\) invariant is a simple complex Lie algebra \(\mathfrak {o}_{2n+1}({{\,\mathrm{\mathbb {C}}\,}})\) of type \(\mathrm {B}_{n},\) with root system

for an orthonormal basis \(e_1,\hdots ,e_n\) of \({{\,\mathrm{{\mathbb {R}}}\,}}^n.\) Fix k with \(1{<}k{<}n.\) The cross-marked Dynkin diagram

represents the grassmannian of totally \(\mathfrak {b}\)-isotropic k-planes in \({{\,\mathrm{\mathbb {C}}\,}}^{2n+1}.\) Here \(\upalpha _{i}{=}e_{i}{-}e_{i+1}\) for \(1{\le }i{<}n\) and \(\upalpha _{n}\,{=}\,e_{n}.\) We have \(\Phi \,{=}\,\{\upalpha _{k}\}\) and
Real forms are obtained by fixing a conjugation \(\upsigma \) on \({{\,\mathrm{\mathbb {C}}\,}}^{2n+1}.\) Then

is hermitian symmetric and nondegenerate, of signature (p, q) for a pair of nonnegative integers with \(p{+}q{=}2n{+}1.\) The Lie algebra of the group of \({{\,\mathrm{\mathbb {C}}\,}}\)-linear transformations which keep fixed both \(\mathfrak {b}\) and \(\mathfrak {b}_{\upsigma }\) is a real form \({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma }\) of \({{\,\mathrm{\mathfrak {s}}\,}}{\simeq }\mathfrak {o}_{2n+1}({{\,\mathrm{\mathbb {C}}\,}}),\) which is isomorphic to the real simple Lie algebra \(\mathfrak {o}(p,q).\)
We define a conjugation \(\upsigma \) on  by
by
According to the number of compact roots between \(e_{2},\hdots ,e_{n-1},\) this conjugation corresponds to any of the Lie algebras \(\mathfrak {o}(p,2n{+}1-p)\) with \(1{\le }p{\le }2n.\) The orbit \(\textsf {M}_{\Phi ,\upsigma }\) consists of \(\mathfrak {b}_{\upsigma }\)-isotropic k-spaces \(\ell _{k}\) with \(\dim (\ell _{k}\cap \upsigma (\ell _{k})){=}k{-}1.\) By (1.13), since \(\mathfrak {q}_{\Phi }\) is maximal, if the parabolic CR algebra \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is fundamental and not totally complex, then it is also weakly nondegenerate. To compute its Levi order we observe that
The fact that \(\texttt {Q}_{\Phi }^{c}\cap {\bar{\texttt {Q}}}_{\Phi }^{c}{\ne }\emptyset \) shows that \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is not totally complex.
Since \(e_{n}\,{\in }\,{\texttt {Q}}_{\Phi }\cap {\bar{\texttt {Q}}}_{\Phi }^{c}\) and \(e_{1}\,{\in }\, {\bar{\texttt {Q}}}_{\Phi }\cap \texttt {Q}_{\Phi }^{c}\) add up to \(e_{1}{+}e_{n},\) the CR algebra \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is fundamental and therefore, as we noticed above, weakly nondegenerate.
The roots \(\upbeta _{i}\,{=}\,-(e_{1}{+}e_{i}),\) for \(2{\le }i{\le }k\) belong to \({\texttt {Q}}_{\Phi }\cap {\bar{\texttt {Q}}}_{\Phi }^{c}\) and have \(\upxi _{\Phi }(\upbeta _{i})\,{=}\,{-}2.\) Since \(\upxi _{\Phi }(e_{1}{+}e_{2})\,{=}\,1\) and \(\upxi _{\Phi }(\upalpha )\,{\le }\,1\) for all \(\upalpha \,{\in }\,{\bar{\texttt {Q}}}_{\Phi }\cap \texttt {Q}_{\Phi }^{c},\) no chain (2.11) that added up to \(\upbeta _{i}\) yields \(e_{1}{+}e_{n}\) contains less than three elements. By Theorem 2.11 this shows that \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) has Levi order 3. We have indeed
Example 2.13
Consider a simple complex Lie algebra \({{\,\mathrm{\mathfrak {s}}\,}}\) of type \(\mathrm {D}_{4}.\) Its root system is described, by using an orthonormal basis \(e_{1},e_{2},e_{3},e_{4}\) of \({{\,\mathrm{{\mathbb {R}}}\,}}^{4},\) by

Consider the complex flag manifold \(\textsf {F}_{\Phi }\) corresponding to the cross-marked Dynkin diagram

with \(\upalpha _{1}=e_{1}-e_{2},\) \(\upalpha _{2}=e_{2}-e_{3},\) \(\upalpha _{3}=e_{3}-e_{4},\) \(\upalpha _{4}=e_{3}+e_{4}\) and \(\Phi \,{=}\,\{\upalpha _{2}\}.\)
It is the grassmannian of projective lines contained in the nondegenerate quadric complex hypersurface in \(\mathbb {CP}^{7}.\) The grading functional is
Take the conjugation
We have
This shows that \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is not totally complex and therefore, since \(\mathfrak {q}_{\Phi }\) is maximal parabolic, this CR algebra is weakly nondegenerate iff it is fundamental. We have
Note that \(e_{3}{+}e_{4}\,{\in }\,\texttt {Q}_{\Phi }\cap {\bar{\texttt {Q}}}^{c}\) and \(e_{1}{-}e_{3}\,{\in }\, {\bar{\texttt {Q}}}\,{\cap }\,\texttt {Q}^{c}\) sum up to \(e_{1}{+}e_{4}.\) This shows that \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is not totally complex and fundamental. Since \(\mathfrak {q}_{\Phi }\) is maximal parabolic, this implies that \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is weakly nonedegenerate.
The root \(\upbeta {=}{-}e_{1}{-}e_{2}\) belongs to \(\texttt {Q}_{\Phi }\,{\cap }\, {\bar{\texttt {Q}}}^{c}_{\Phi }\) and \(\upxi _{\Phi }(\upbeta )\,{=}\,{-}2.\) Since all roots \(\upalpha \) in \({\bar{\texttt {Q}}}_{\Phi }\,{\cap }\,\texttt {Q}^{c}_{\Phi }\) distinct from \(e_{1}{+}e_{2}\) have \(\xi _{\upbeta }(\upalpha ){=}1,\) a sequence satisfying (2.11) and summing up with \(\upbeta \) to \(\{e_{1}{+}e_{4}\}\) contains at least 3 elements. By Theorem 2.11 this shows that \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) has Levi order 3. An admissible sequence for \({-}e_{1}{-}e_{2}\) is \( (e_{1}{-}e_{3},\; e_{1}{+}e_{3},\; e_{2}{+}e_{4}). \)
Example 2.14
Consider a semisimple complex Lie algebra \({{\,\mathrm{\mathfrak {s}}\,}}\) of type \(\mathrm {G}_{2}.\) Having fixed a Cartan subalgebra, we can write its root system in the form

for an orthonormal basis \(e_{1},e_{2},e_{3}\) of \({{\,\mathrm{{\mathbb {R}}}\,}}^{3}.\) We consider the complex flag manifold \(\textsf {F}_{\Phi }\) corresponding to the cross-marked Dynkin diagram

It corresponds to the grading functional \(\upxi _{\Phi }\) with
We consider the conjugation defined by
Then
Since \(\mathfrak {q}_{\Phi }\) is maximal and \(\texttt {Q}^{c}_{\Phi }\,{\cap }\,{\bar{\texttt {Q}}}^{c}_{\Phi }{\ne }\emptyset ,\) then is sufficient to check that \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is weakly nondegenerate to find that it is also fundamental.
The root \(\upbeta \,{=}\, 2e_{3}{-}e_{1}{-}e_{2}\) belongs to \(\texttt {Q}_{\Phi }\,{\cap }\,{\bar{\texttt {Q}}}^{c}_{\Phi }.\) We have
Since \(\upxi _{\Phi }\) equals one on every root of \(\texttt {Q}^{\,c}_{\Phi }\,{\cap }\, {\bar{\texttt {Q}}}_{\Phi },\) a sequence satisfying (2.11) has at least three roots. We find indeed that
is a sequence with the desired properties, proving that \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is fundamental and has Levi order three.
3.6 Levi order of orbits of the minimal type
Weak nondegeneracy for minimal orbits was characterized in [1, Thm.11.5] by using their description in terms of cross-marked Satake diagrams (see e.g. [5, 24]).
Let \(\mathfrak {h}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) be a maximally vectorial Cartan subalgebra of \({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\) \(\mathfrak {h}\) its complexification and  the root system of \(({{\,\mathrm{\mathfrak {s}}\,}},\mathfrak {h}).\) Then all roots in
the root system of \(({{\,\mathrm{\mathfrak {s}}\,}},\mathfrak {h}).\) Then all roots in  are compact. We can select a basis
are compact. We can select a basis  such that the conjugate of any positive noncompact root stays positive. This condition defines an involution
such that the conjugate of any positive noncompact root stays positive. This condition defines an involution  which keeps fixed the elements of
which keeps fixed the elements of  and such that, for nonnegative \(n_{\upalpha ,\upbeta }{\in }{{\,\mathrm{\mathbb {Z}}\,}},\)
and such that, for nonnegative \(n_{\upalpha ,\upbeta }{\in }{{\,\mathrm{\mathbb {Z}}\,}},\)

The Satake diagram  is obtained from
is obtained from  by painting black the roots in
by painting black the roots in  and joining by an arch the pairs of distinct simple roots \(\upalpha _{1},\upalpha _{2}\) with \(\epsilon (\upalpha _{1})=\upalpha _{2}.\)
and joining by an arch the pairs of distinct simple roots \(\upalpha _{1},\upalpha _{2}\) with \(\epsilon (\upalpha _{1})=\upalpha _{2}.\)
Minimal orbits correspond to cross-marked Satake diagrams: they are associated to parabolic \(\mathfrak {q}_{\Phi }\) for which all roots in \(\texttt {Q}_{\Phi }^{\,c}{\cap }\,{\bar{\texttt {Q}}}_{\Phi }^{\,n}\) are compact.
Let us drop the assumption that \(\mathfrak {h}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) is maximally vectorial. The map \(\uptheta \,{:}\,\upalpha \,{\mapsto }\,{-}{\bar{\upalpha }}\) induced on  by the Cartan involution (see Sect. 2.2) acts on \(\texttt {Q}_{\Phi }^{\,c}\cap {\bar{\texttt {Q}}}^{\,n}_{\Phi }\), which is therefore the union of its fixed points, which are roots in
by the Cartan involution (see Sect. 2.2) acts on \(\texttt {Q}_{\Phi }^{\,c}\cap {\bar{\texttt {Q}}}^{\,n}_{\Phi }\), which is therefore the union of its fixed points, which are roots in  , and of pairs \((\upalpha ,{-}{\bar{\upalpha }})\) of distinct roots.
, and of pairs \((\upalpha ,{-}{\bar{\upalpha }})\) of distinct roots.
Definition 2.4
We say that the CR algebra \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) and the corresponding CR manifold \(\textsf {M}_{\Phi ,\upsigma }\) are of the minimal type if the roots in \(\texttt {Q}_{\Phi }^{\,c}\cap {\bar{\texttt {Q}}}^{\,n}_{\Phi }\) are fixed by the Cartan involution, i.e. if

Lemma 2.15
For a parabolic CR algebra \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) the following are equivalent to the fact that it is of the minimal type:


Proof
(2.19) is equivalent to (2.20). Indeed, since \(\upxi _{\Phi }({\bar{\upbeta }})\,{\le }\,0\) for all \(\upbeta \,{\in }{\bar{\texttt {Q}}}_{\Phi },\) clearly (2.19) is a consequence of (2.20). The two are equivalent because \(\upxi _{\Phi }({\bar{\upbeta }}){>}0\) for \(\upbeta \,{\in }\,{\bar{\texttt {Q}}}^{\,c}_{\Phi }\) and  The equivalence of (2.18) with (2.19) reduces to the observation that the elements of \(\texttt {Q}_{\Phi }^{\,c}\) on which \(\upxi _{\Phi }{\circ }\,\upsigma \) is negative make the set \(\texttt {Q}^{\,c}_{\Phi }\cap {\bar{\texttt {Q}}}^{\,n}_{\Phi }\). \(\square \)
The equivalence of (2.18) with (2.19) reduces to the observation that the elements of \(\texttt {Q}_{\Phi }^{\,c}\) on which \(\upxi _{\Phi }{\circ }\,\upsigma \) is negative make the set \(\texttt {Q}^{\,c}_{\Phi }\cap {\bar{\texttt {Q}}}^{\,n}_{\Phi }\). \(\square \)
Example 2.16
Keep the notation of Example 2.12. The cross-marked Dynkin diagram of \(\mathrm {B}_{3}\)

corresponds to
Consider the conjugation
Since  by Proposition 2.2 the CR algebra \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is fundamental. We have
by Proposition 2.2 the CR algebra \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is fundamental. We have
This \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is of the minimal type, because

However, \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is not the CR algebra of the minimal orbit of a real form of \(\mathbf {SO}_{7}({{\,\mathrm{\mathbb {C}}\,}})\) in \(\textsf {F}_{\Phi },\) because, although  and \({\bar{\upalpha }}_{2}{=}\upalpha _{1}{+}\upalpha _{2}{+}2\upalpha _{3} \,{\succ }\,0,\) showing that the basis \(\upalpha _{1},\upalpha _{2},\upalpha _{3}\) defines an S-chamber according to [3], the diagram obtained by blackening the nodes \(\upalpha _{1},\upalpha _{3}\) is not Satake. The equalities
and \({\bar{\upalpha }}_{2}{=}\upalpha _{1}{+}\upalpha _{2}{+}2\upalpha _{3} \,{\succ }\,0,\) showing that the basis \(\upalpha _{1},\upalpha _{2},\upalpha _{3}\) defines an S-chamber according to [3], the diagram obtained by blackening the nodes \(\upalpha _{1},\upalpha _{3}\) is not Satake. The equalities
show that \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is weakly nondegenerate.
We can choose real forms \(\mathbf {SO}(2,5)\) or \(\mathbf {SO}(3,4)\) compatible with the complex symmetric bilinear form \(\mathfrak {b}\) used to define \(\mathbf {SO}_{7}({{\,\mathrm{\mathbb {C}}\,}}).\) Then \(\textsf {M}_{\Phi ,\upsigma }\) consists of pairs \((\ell _{1}\,{\subset }\,\ell _{3})\) with a \(\mathfrak {b}_{\upsigma }\)-isotropic \(\ell _{1}\) with \(\ell _{1}{\cap }{\bar{\ell }}_{1}\,{=}\,\{0\}\) and an \(\ell _{3}\) on which the restriction of \(\mathfrak {b}_{\upsigma }\) has rank 1.
Theorem 2.17
A real orbit \(\textsf {M}_{\Phi ,\upsigma }\) of the minimal type is either holomorphically degenerate or has Levi order less or equal two.
Proof
Let \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) be a parabolic CR algebra of the minimal type. Keeping the notation used throughout the section, we note that (2.18) can be rewritten in the form

Let \(\upbeta \,{\in }\,\texttt {Q}_{\Phi }\,{\cap }\,{\bar{\texttt {Q}}}_{\Phi }^{\,c}.\) If  then \(\upxi _{\Phi }(\upbeta )\,{=}\,0\) by (\(*\)) and hence, by Corollary 2.8,
then \(\upxi _{\Phi }(\upbeta )\,{=}\,0\) by (\(*\)) and hence, by Corollary 2.8,  is either 1 or \({+}\infty .\)
is either 1 or \({+}\infty .\)
Let us consider now the case where  is an integer \(q{>}1.\) Then
is an integer \(q{>}1.\) Then  Let \((\upalpha _{1},\hdots ,\upalpha _{q})\) be a sequence satisfying (2.11) and thus the conditions in Lemma 2.6. Since
Let \((\upalpha _{1},\hdots ,\upalpha _{q})\) be a sequence satisfying (2.11) and thus the conditions in Lemma 2.6. Since  there is at least one root \(\upalpha _{i}\) which does not belong to
there is at least one root \(\upalpha _{i}\) which does not belong to  By the Lemma we can assume it is \(\upalpha _{1}.\) Then \(\upbeta {+}\upalpha _{1}\) belongs to
By the Lemma we can assume it is \(\upalpha _{1}.\) Then \(\upbeta {+}\upalpha _{1}\) belongs to  and therefore, by the first part of the proof,
and therefore, by the first part of the proof,  This implies that \(q{=}2.\) The proof is complete. \(\square \)
This implies that \(q{=}2.\) The proof is complete. \(\square \)
Lemma 2.18
The parabolic CR algebra \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) of a minimal orbit is of the minimal type.
Proof
Suppose that \(\Phi \) is the set of crossed roots in a cross-marked Satake diagram. Since all roots \(\upbeta \) in \(\texttt {Q}^{\,c}_{\Phi }\) are positive, by (2.17), if  then its conjugate \({\bar{\upbeta }}\) is positive, and hence has \(\upxi _{\Phi }(\upbeta ){\ge }0.\) This shows that (2.18) is valid, i.e. that \(\textsf {M}_{\Phi ,\upsigma }\) is of the minimal type. \(\square \)
then its conjugate \({\bar{\upbeta }}\) is positive, and hence has \(\upxi _{\Phi }(\upbeta ){\ge }0.\) This shows that (2.18) is valid, i.e. that \(\textsf {M}_{\Phi ,\upsigma }\) is of the minimal type. \(\square \)
Corollary 2.19
A minimal orbit \(\textsf {M}_{\Phi ,\upsigma }\) is either holomorphically degenerate or has Levi order less or equal to two. \(\square \)
Example 2.20
Consider the CR algebra described by the cross-marked Satake diagram

It is associated to the minimal orbit \(\textsf {M}_{\Phi ,\upsigma }\) of \(\mathbf {SU}(1,3)\) is the Grassmannian of isotropic two-planes of \({{\,\mathrm{\mathbb {C}}\,}}^{4}\) for a hermitian symmetric form of signature (1, 3).
Here \({{\,\mathrm{\mathfrak {s}}\,}}\,{\simeq }\,\mathfrak {sl}_{4}({{\,\mathrm{\mathbb {C}}\,}}),\) 
 \(\{\{e_{1}{-}e_{2},\,e_{2}{-}e_{3},\,e_{3}{-}e_{4}\}\) for an orthonormal basis \(e_{1},e_{2},e_{3},e_{4}\) of \({{\,\mathrm{{\mathbb {R}}}\,}}^{4},\) \(\Phi \,{=}\,\{e_{2}{-}e_{3}\}\),
\(\{\{e_{1}{-}e_{2},\,e_{2}{-}e_{3},\,e_{3}{-}e_{4}\}\) for an orthonormal basis \(e_{1},e_{2},e_{3},e_{4}\) of \({{\,\mathrm{{\mathbb {R}}}\,}}^{4},\) \(\Phi \,{=}\,\{e_{2}{-}e_{3}\}\),
We obtain
Since \(\texttt {Q}^{c}_{\Phi }\cap {\bar{\texttt {Q}}}^{c}_{\Phi }\) is nonempty, \(e_{1}{-}e_{4}\,{=}\,(e_{3}{-}e_{4}){+}(e_{1}{-}e_{3})\) and \(\mathfrak {q}_{\Phi }\) is maximal, we obtain that \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is fundamental and weakly nondegenerate. Since \(\upxi _{\Phi }(e_{3}{-}e_{2}){=}{-}1\) and \(\upxi _{\Phi }\) is 1 on all the elements of \({\bar{\texttt {Q}}}_{\Phi }\cap \texttt {Q}^{c}_{\Phi },\) the Levi order is at least, and thus equal, by Theorem 2.17, to 2. We have in fact
Example 2.21
Consider the CR algebra described by the cross-marked Satake diagram

Here  , \(\upalpha _{i}\,{=}\,e_{i}{-}e_{i+1},\) \(\Phi \,{=}\,\{\upalpha _{3}\},\)
, \(\upalpha _{i}\,{=}\,e_{i}{-}e_{i+1},\) \(\Phi \,{=}\,\{\upalpha _{3}\},\)
It corresponds to the CR algebra \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi }),\) with \({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma }\,{\simeq }\,\mathfrak {sl}_{3}(\mathbb {H}),\) of the grassmannian \(\textsf {M}_{\Phi ,\upsigma }\) of 3-planes of \({{\,\mathrm{\mathbb {C}}\,}}^{6}\,{\simeq }\,\mathbb {H}^{3}\) containing a quaternionic line. We have
Since \(\mathfrak {q}_{\Phi }\) is maximal, it suffices to note that \((e_{4}{-}e_{5}){+}(e_{1}{-}e_{4}){=} e_{1}{-}e_{5}\,{\in }\,\texttt {Q}^{\,c}_{\Phi }\cap {\bar{\texttt {Q}}}^{\,c}_{\Phi }\) to conclude that \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is fundamental and weakly nondegenerate.
We have  Since both
Since both
we get  showing that the Levi order of \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) equals two.
showing that the Levi order of \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) equals two.
Example 2.22
The CR algebra described by the cross-marked Satake diagram

corresponding to \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi }),\) with \({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma }\,{\simeq }\,\mathfrak {sl}_{7}({{\,\mathrm{\mathbb {C}}\,}}),\) is fundamental and weakly nondegenerate. This can be proved e.g. by applying the criteria in [1]. Since  its Levi order is one.
its Levi order is one.
Example 2.23
Keep the notation of Example 2.12 and consider the cross-marked Dynkin diagram of \(\mathrm {B}_{3}\)

corresponding to
Consider the conjugation
Then, for the corresponding CR algebra \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\), we have
Since \(\upxi _{\Phi }(\upgamma ){=}1\) for all \(\upgamma \,{\in }\,\texttt {Q}^{\,c}_{\Phi }\cap {\bar{\texttt {Q}}}_{\Phi },\) and \(\upxi _{\Phi }(\upgamma ){\ge }{-}1\) for all \(\upgamma \,{\in }\,\texttt {Q}^{\,c}_{\Phi }\cap {\bar{\texttt {Q}}}_{\Phi },\) the Levi order of \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is two. Then \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is a CR algebra is of the minimal type, although is not the CR algebra of a minimal orbit.
Remark 2.24
It was observed in [3] that a parabolic CR algebra \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) can always be described by using a base  associated to an S-chamber: this means one with \({\bar{\upalpha }}\,{\succ }\,0\) for all
associated to an S-chamber: this means one with \({\bar{\upalpha }}\,{\succ }\,0\) for all  The condition of being of the minimal type translates for this choice of
The condition of being of the minimal type translates for this choice of  into the fact that \({\bar{\upalpha }}\,{\succ }\,0\) also for the elements in
into the fact that \({\bar{\upalpha }}\,{\succ }\,0\) also for the elements in  The real dimension of \(\textsf {M}_{\Phi ,\upsigma }\) is the difference \(\dim _{{{\,\mathrm{\mathbb {C}}\,}}}({{\,\mathrm{\mathfrak {s}}\,}}){-}\dim _{{{\,\mathrm{\mathbb {C}}\,}}}(\mathfrak {q}_{\Phi }{\cap }{\bar{\mathfrak {q}}}_{\Phi }),\) i.e.
The real dimension of \(\textsf {M}_{\Phi ,\upsigma }\) is the difference \(\dim _{{{\,\mathrm{\mathbb {C}}\,}}}({{\,\mathrm{\mathfrak {s}}\,}}){-}\dim _{{{\,\mathrm{\mathbb {C}}\,}}}(\mathfrak {q}_{\Phi }{\cap }{\bar{\mathfrak {q}}}_{\Phi }),\) i.e.  . Thus, in case \(\Phi \) contains a root
. Thus, in case \(\Phi \) contains a root  with \({\bar{\upalpha }}\,{\prec }\,0,\) the symmetry with respect to \(\upalpha \) yields a new basis
with \({\bar{\upalpha }}\,{\prec }\,0,\) the symmetry with respect to \(\upalpha \) yields a new basis  that, with the crosses in the same positions, describes a new real orbit whose dimension is smaller by one unit. Then, parametrizing the real orbits that we can describe, after having made a fixed choice of \(\mathfrak {h}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\), by using the Weyl chambers of
that, with the crosses in the same positions, describes a new real orbit whose dimension is smaller by one unit. Then, parametrizing the real orbits that we can describe, after having made a fixed choice of \(\mathfrak {h}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\), by using the Weyl chambers of  those of the minimal type are a sort of local minima with respect to dimension. One has to be cautious because, unless \(\mathfrak {h}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) is maximally vectorial, there can be several inequivalent choices of
those of the minimal type are a sort of local minima with respect to dimension. One has to be cautious because, unless \(\mathfrak {h}_{{{\,\mathrm{{\mathbb {R}}}\,}}}\) is maximally vectorial, there can be several inequivalent choices of  such that \({\bar{\upalpha }}\,{\succ }\,0\) for all
such that \({\bar{\upalpha }}\,{\succ }\,0\) for all  that we can look at as yielding different local minima for the dimension of a class of real orbits.
that we can look at as yielding different local minima for the dimension of a class of real orbits.
3.7 Further examples
We already showed that there are weakly nondegenerate CR algebras \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) of Levi order 3, which, by Theorem 2.17, are not of the minimal type. In this subsection we exhibit examples of weakly nondegenerate parabolic CR algebras which are not of the minimal type and have Levi orders 1, 2.
Example 2.25
Consider \(\mathfrak {sl}_{3}({{\,\mathrm{\mathbb {C}}\,}})\) as a simple real Lie algebra. Its complexification is the direct sum of two copies of \(\mathfrak {sl}_{3}({{\,\mathrm{\mathbb {C}}\,}}).\) Its root system can be described, after fixing orthogonal basis \(e_{1},e_{2},e_{3},e_{4}\) and \(e'_{1},e'_{2},e'_{3},e'_{4}\) of two copies of \({{\,\mathrm{{\mathbb {R}}}\,}}^4,\) by

Let us consider the cross-marked Dynkin diagram

where \(\upalpha _i{=}(e_{i}{-}e_{i+1})\) and \(\upalpha '_i{=}(e'_{i}{-}e'_{i+1}),\) with \(\Phi {=}\{\upalpha _1,\upalpha _3\}{\cup }\{\upalpha '_1,\upalpha '_3\}.\)
Let us fix the conjugation
Then
Since all roots in \(\Phi \) have a negative conjugate, the parabolic CR algebra \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is fundamental. It is not of the minimal type because  and
and
Let us check that \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) has Levi order 1. We get indeed
This also shows that \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is weakly nondegnerate. The orbit \(\textsf {M}_{\Phi ,\upsigma }\) is a CR manifold of CR dimension 6 and CR codimension 4. Its points are quadruples \((\ell _{1},\ell _{1}',\ell _{3},\ell _{3}')\) of linear subspaces of a \({{\,\mathrm{\mathbb {C}}\,}}^{4}\,{\simeq }\,\mathbb {H}^{2}\) with \(\ell _{1},\ell '_{1}\) complex lines such that \(\ell _1{+}\ell _{1}'\) is a quaternionic line and \(\ell _{3},\,\ell _{3}'\) complex hypersurfaces with \(\ell _{3}{\cap }\ell '_{3}\,{=}\,\ell _1{+}\ell '_{1}.\)
Example 2.26
Consider a root system

of type \(\mathrm {D}_{4}\) and the maximal parabolic \(\mathfrak {q}_{\Phi }\) described by the cross-marked Dynkin diagram

Here \(\upalpha _{i}{=}e_{i}{-}e_{i+1},\) for \(1{\le }i{\le }3\) and \(\upalpha _4{=}e_{3}{+}e_{4},\) \(\Phi \,{=}\,\{\upalpha _{2}\},\)
With the conjugation
we obtain

It is easy to check, using the fact that \(\mathfrak {q}_{\Phi }\) is maximal, that \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is fundamental and weakly nondegenerate; moreover the last line of the equalities above shows that \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is not of the minimal type. To check that \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is Levi nondegenerate (i.e. has Levi order 1) we observe that
Example 2.27
Consider a root system

of type \(\mathrm {C}_{3}\) and the cross-marked Dynkin diagram

with \(\upalpha _1{=}e_{1}{-}e_2,\) \(\upalpha _{2}{=}e_2{-}e_3,\) \(\upalpha _{3}{=}2e_{3}\) and \(\Phi =\{\upalpha _{2}\}\) so that
Consider the conjugation
We obtain
Since the parabolic \(\mathfrak {q}_{\Phi }\) is maximal, it is easy to check that \(({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma },\mathfrak {q}_{\Phi })\) is fundamental and weakly nondegenerate. It has Levi order two, as one can check from
4 Weakly nondegenerate CR manifolds with larger Levi orders
Fix any integer  In this last section we discuss in detail the example of a homogeneous CR manifold \(\textsf {M}\) of CR dimension
In this last section we discuss in detail the example of a homogeneous CR manifold \(\textsf {M}\) of CR dimension  and CR codimension 1 which is fundamental and weakly nondegenerate of Levi order
and CR codimension 1 which is fundamental and weakly nondegenerate of Levi order  .
.
The compact group \(\mathbf {SU}(2)\) acts transitively on the complex projective line \(\mathbb {CP}^{1}.\) The homogeneous complex structure of \(\mathbb {CP}^{1}\) can be defined by the totally complex CR algebra \((\mathfrak {su}(2),\mathfrak {b}),\) where \(\mathfrak {su}(2)\) is the real Lie algebra of anti-Hermitian \(2{\times }2\) matrices and \(\mathfrak {b}\) a Borel subalgebra of its complexification \(\mathfrak {sl}_{2}({{\,\mathrm{\mathbb {C}}\,}}).\) This CR algebra corresponds to the simple cross-marked Satake diagram

The root system of the complexification \(\mathfrak {sl}_{2}({{\,\mathrm{\mathbb {C}}\,}})\) is  and we take \(\upalpha \,{=}\,(e_{1}{-}e_{2}),\) with fundamental weight \(\upomega \,{=}\,\upalpha /2.\)
and we take \(\upalpha \,{=}\,(e_{1}{-}e_{2}),\) with fundamental weight \(\upomega \,{=}\,\upalpha /2.\)
With our usual notation, \(\Phi {=}\{\upalpha \},\) so that \(\mathfrak {b}\,{=}\,\mathfrak {q}_{\Phi }\); moreover \(\upxi _{\Phi }(e_{i}){=}({-}1)^{{i+1}}/2\) and \({{\,\mathrm{\mathfrak {s}}\,}}_{\upsigma }{=}\mathfrak {su}_{2},\) with conjugation \(\upsigma (e_{1}){=}e_{2},\) \(\upsigma (e_{2})=e_{1}.\)
The irreducible finite dimensional complex linear representations of \(\mathfrak {sl}_{2}({{\,\mathrm{\mathbb {C}}\,}})\) are indexed by the nonnegative integral multiples \(k{\cdot }\upomega \) of \(\upomega \) and the corresponding irreducible \(\mathfrak {sl}_{2}({{\,\mathrm{\mathbb {C}}\,}})\)-module \(\textsf {V}_{k{\cdot }\upomega }\) can be identified with the space of complex homogeneous polynomials of degree k in two indeterminates
We have
where, for a diagonal H in the canonical Cartan subalgebra of \(\mathfrak {sl}_{2}({{\,\mathrm{\mathbb {C}}\,}}),\)

are the one-dimensional weight spaces contained in \(\textsf {V}_{k\upomega }.\)
Since \({\bar{\upomega }}{=}-\upomega ,\) we have \({\overline{\textsf {V}}}_{k\upomega }\,{=}\,\textsf {V}_{k\upomega }.\) The anti-\({{\,\mathrm{\mathbb {C}}\,}}\)-linear automorphism \(\uptheta _{k\upomega }\) of \(\textsf {V}_{k\upomega }\) defined by the conjugation \(\upsigma \) comes from \((z,w)\,{\mapsto }\,({-}{\bar{w}},{\bar{z}})\) and therefore
Then \(\uptheta _{k\upomega }^{2}\) equals \(\mathrm {id}_{\textsf {V}_{k\upomega }}\) for k even and \({-}\mathrm {id}_{\textsf {V}_{k\upomega }}\) for k odd. Accordingly, for k even \(\textsf {V}_{k\upomega }\) is the complexification of an irreducible \((k{+}1)\)-dimensional representation of the real type, that we will denote by \(\textsf {V}^{{{\,\mathrm{{\mathbb {R}}}\,}}}_{k\upomega }\); for k odd is isomorphic to a \(2(k{+}1)\)-dimensional irreducible representation of the quaternionic type of \(\mathfrak {su}_{2}\) (see e.g. [7, Ch.IX, App.II, Prop.2]).
Remark 3.1
Studying irreducible representation of \(\mathfrak {su}_2\) turns out to be of some interest in quantum physics, as they arise when considering rotations on fermionic and bosonic systems (for more details see [26, Ch.5 , §5]).
The subspace
is a \(\mathfrak {b}\)-submodule of \(\textsf {V}_{k\upomega }\) and we can consider the semidirect sum \(\mathfrak {b}\,{\oplus }\,\textsf {V}_{k\upomega }^{-}\) as a subalgebra of the abelian extension \(\mathfrak {sl}_{2}({{\,\mathrm{\mathbb {C}}\,}})\,{\oplus }\,\textsf {V}_{k\upomega }\) (cf. e.g. [23, Ch.VII,§3]). We may consider the map \(\mathbf {SL}_{2}({{\,\mathrm{\mathbb {C}}\,}})\rightarrow \mathbb {CP}^{1}\) associated to our choice of a Borel subalgebra \(\mathbf {B}\) as a principal bundle with structure group \(\mathbf {B}.\) Then the Lie pair \((\mathfrak {sl}_{2}({{\,\mathrm{\mathbb {C}}\,}})\,{\oplus }\,\textsf {V}_{k\upomega },\mathfrak {b}\,{\oplus }\,\textsf {V}_{k\upomega }^{-})\) defines a complex holomorphic vector bundle \(\textsf {E}_{k}\) with base \(\mathbb {CP}^{1}\) and typical fiber \(\textsf {V}_{k\upomega }/\textsf {V}_{k\upomega }^{-}{\simeq }{\bigoplus }_{2h{\le }k}\textsf {V}_{k\upomega }^{(k-2h)\upomega }\) (this is an example of Mostow fibration, see e.g. [20] and the bibliography there in).
Proposition 3.2
Let  be any positive integer. Then
be any positive integer. Then

is the CR algebra of a CR manifold \(\textsf {E}_{2q}\), of CR dimension \(q{+}1\) and CR codimension 1, which is fundamental and weakly nondegnenerate of Levi order 
Proof
We have

If \(Z_{\upalpha },Z_{-\upalpha },H\) is the canonical basis of \(\mathfrak {sl}_{2}({{\,\mathrm{\mathbb {C}}\,}})\) and  a nonzero vector of
a nonzero vector of  then the images of
then the images of  generate \(\mathfrak {q}'_{\Phi }/(\mathfrak {q}'_{\Phi }{\cap }{\bar{\mathfrak {q}}}'_{\Phi }).\) Since
generate \(\mathfrak {q}'_{\Phi }/(\mathfrak {q}'_{\Phi }{\cap }{\bar{\mathfrak {q}}}'_{\Phi }).\) Since

we obtain that  is fundamental and weakly nondegenerate. With the notation of the previous section, we have \(\texttt {Q}_{\Phi }^{\,c}{\cap }{\bar{\texttt {Q}}}_{\Phi }{=}\{\upalpha \},\) with \(\upxi _{\Phi }(\upalpha ){=}1\) and \(\upxi _{\Phi }(-2j\upomega ){=}{-}j.\) Since \(\mathfrak {g}/(\mathfrak {q}'_{\Phi }{+}{\bar{\mathfrak {q}}}'_{\Phi })\) is generated by the image of
is fundamental and weakly nondegenerate. With the notation of the previous section, we have \(\texttt {Q}_{\Phi }^{\,c}{\cap }{\bar{\texttt {Q}}}_{\Phi }{=}\{\upalpha \},\) with \(\upxi _{\Phi }(\upalpha ){=}1\) and \(\upxi _{\Phi }(-2j\upomega ){=}{-}j.\) Since \(\mathfrak {g}/(\mathfrak {q}'_{\Phi }{+}{\bar{\mathfrak {q}}}'_{\Phi })\) is generated by the image of  by the above considerations the Levi order of an element of
by the above considerations the Levi order of an element of  equals j. This shows that the Levi order of \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q}'_{\Phi })\) is
equals j. This shows that the Levi order of \((\mathfrak {g}_{{{\,\mathrm{{\mathbb {R}}}\,}}},\mathfrak {q}'_{\Phi })\) is  \(\square \)
\(\square \)
In an analogous way we can also prove
Proposition 3.3
For each positive integer  , the homogeneous CR manifold
, the homogeneous CR manifold  is contact nondegenerate of order
is contact nondegenerate of order  \(\square \)
\(\square \)
Remark 3.4
Representations \(\textsf {V}_{k\upomega }\) with an odd k are canonically associated with complex holomorphic vector bundles \(\textsf {E}_{k},\) of rank \((k{+}1),\) with base \(\mathbb {CP}^{1}.\)
References
Altomani, A., Medori, C., Nacinovich, M.: The CR structure of minimal orbits in complex flag manifolds. J. Lie Theory 16(3), 483–530 (2006)
Altomani, A., Medori, C., Nacinovich, M.: On the topology of minimal orbits in complex flag manifolds. Tohoku Math. J. (2) 60(3), 403–422 (2008)
Altomani, A., Medori, C., Nacinovich, M.: Orbits of real forms in complex flag manifolds. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 9(1), 69–109 (2010)
Andreotti, A., Fredricks, G.A.: Embeddability of real analytic Cauchy–Riemann manifolds. Ann. Sc. Norm. Sup. Pisa Cl. Sci. (4) 6(2), 285–304 (1979)
Araki, S.: On root systems and an infinitesimal classification of irreducible symmetric spaces. J. Math. Osaka City Univ. 13, 1–34 (1962)
Bourbaki, N.: Lie groups and Lie algebras. Chapters 4–6, Elements of Mathematics (Berlin), Springer, Berlin (2002). Translated from the 1968 French original by Andrew Pressley
Bourbaki, N.: Lie groups and Lie algebras. Chapters 7–9, Elements of Mathematics (Berlin), Springer, Berlin (2005). Translated from the 1975 and 1982 French originals by Andrew Pressley
Bremigan, R., Lorch, J.: Orbit duality for flag manifolds. Manuscr. Math. 109(2), 233–261 (2002)
Brinkschulte, J., Hill, C.D., Leiterer, J., Nacinovich, M.: Aspects of the Levi form. Boll. Unione Mat. Ital. 13, 71–89 (2020)
Fels, G.: Locally homogeneous finitely nondegenerate CR-manifolds. Math. Res. Lett. 14(6), 893–922 (2007)
Fels, G., Huckleberry, A.T., Wolf, J.A.: Cycle spaces of flag domains, Progress in Mathematics, vol. 245. Birkhäuser Boston Inc., Boston (2006) (A complex geometric viewpoint)
Freeman, M.: Local biholomorphic straightening of real submanifolds. Ann. Math. 106, 319–352 (1977)
Freeman, M.: Real submanifolds with degenerate Levi form, Several complex variables, Part 1, Proc. Sympos. Pure Math., Williams Coll., Williamstown, Mass., 1975, vol. XXX, p. 141–147. Amer. Math. Soc. (1977)
García, A.N., Sánchez, C.U.: On extrinsic symmetric CR-structures on the manifolds of complete flags. Beiträge Algebra Geom. 45(2), 401–414 (2004)
Greenfield, S.: Cauchy–Riemann equations in several variables. Ann. Sc. Norm. Sup. Pisa 22, 275–314 (1968)
Hermann, R.: Convexity and pseudoconvexity for complex manifolds, II. Indiana J. Math. 22, 1065–1070 (1964)
Lotta, A., Nacinovich, M.: On a class of symmetric CR manifolds. Adv. Math. 191(1), 114–146 (2005)
Marini, S., Medori, C., Nacinovich, M., Spiro, A.: On transitive contact and CR algebras. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) XX, 771–795 (2020)
Marini, S., Nacinovich, M.: Orbits of real forms, Matsuki duality and \(CR\)-cohomology, Complex and symplectic geometry, Springer INdAM Ser., vol. 21, pp. 149–162. Springer, Cham (2017)
Medori, C., Nacinovich, M.: Complete nondegenerate locally standard CR manifolds. Math. Ann. 317(3), 509–526 (2000)
Medori, C., Nacinovich, M.: Algebras of infinitesimal CR automorphisms. J. Algebra 287(1), 234–274 (2005)
Newlander, L., Nirenberg, A.: Complex analytic coordinates in almost complex manifolds. Ann. Math 65, 391–404 (1957)
Hilton, P.J., Stammbach, U.: A Course in Homological Algebra, Graduate Texts in Mathematics, vol. 4. Springer, New York (1971)
Satake, I.: On representations and compactifications of symmetric Riemannian spaces. Ann. Math. 71, 77–110 (1960)
Tanaka, N.: On differential systems, graded Lie algebras and pseudogroups. J. Math. Kyoto Univ. 10, 1–82 (1970)
Tinkham, M.: Group Theory and Quantum Mechanics. McGraw-Hill, New York (1964)
Wolf, J .A.: The action of a real semisimple group on a complex flag manifold. I. Orbit structure and holomorphic arc components. Bull. Am. Math. Soc. 75, 1121–1237 (1969)
Funding
Open Access funding provided by Universit... degli Studi di Parma.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research has financially been supported by PRIN 2017 “Real and Complex Manifolds: Geometry, Topology and Harmonic Analysis” and the Programme FIL-Quota Incentivante of University of Parma and co-sponsored by Fondazione Cariparma.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Marini, S., Medori, C. & Nacinovich, M. Higher order Levi forms on homogeneous CR manifolds. Math. Z. 299, 563–589 (2021). https://doi.org/10.1007/s00209-020-02691-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00209-020-02691-6




 if
if  ;
; if
if 
 ;
; at x, then it has also finite contact order
at x, then it has also finite contact order  with
with 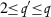 at x.
at x.  if
if 
 for all integers
for all integers 
 if
if 
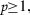
 is a Lie algebra and, for
is a Lie algebra and, for  an ideal of
an ideal of  be the complexification of
be the complexification of  Then
Then 
 for all integers
for all integers 
 if and only if
if and only if 
 specifying the parabolic subalgebra
specifying the parabolic subalgebra  ;
; of
of 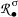 into a first set consisting of the compact and a second of the hermitian roots.
into a first set consisting of the compact and a second of the hermitian roots. ;
; ;
; ;
;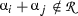 for all
for all 